时政课程	2019重要会议时政考点梳理直播课  2019时政一点通
鲁考课程	2019鲁考（山东公务员）面授课程  鲁考系统直播课     网校笔试课程
选调课程	2019选调笔试辅导课程  选调笔试网校课程
非统考事业单位	2019事业单位笔试辅导课程（综合、卫生类） 网校课程
非统考教师课程	2019教师招聘笔试辅导课程  网校课程
推荐阅读	2020国考笔试课程  2020成公协议课程    三支一扶笔试课程   1对1专业定制课程

联创世华统一客服热线：4001105311

联创世华总部及十七地市联系方式（点击查看）

2019公职考试行测科目每日一练（4月10日）

1．假设空气质量可按良好、轻度污染和重度污染三类划分。一环境监测单位在某段时间对63个城市的空气质量进行了监测，结果表明：空气质量良好城市数是重度污染城市数的3倍还多3个，轻度污染城市数是重度污染城市数的2倍。那么空气质量良好的城市个数是（  ）

A．33         B．31         C．23         D．27

2．同样价格的某商品在4个商场销售时都进行了两次价格调整。甲商场第一次提价的百分率为a，第二次提价的百分率为b（a>0，b>0，且ab）；乙商场两次提价的百分率均为（a+b）；丙商场第一次提价的百分率为（a+b），第二次提价的百分率为（a+b）；丁商场第一次提价的百分率为b，第二次提价的百分率为a，两次提价后该商品售价最高的商场是（  ）

A．甲商场         B．乙商场         C．丙商场         D．丁商场

3．黑白两个盒子中共有棋子193颗。若从白盒子中取出15颗棋子放入黑盒子中，则黑盒子中的棋子数是白盒子中棋子数的m（m为正整数）倍还多6颗。那么，黑盒子中原来的棋子至少有（  ）

A．121颗         B．140颗         C．161颗         D．167颗

4．一实心圆锥体的底面半径为r，母线长为2r。若截圆锥体得到两个同样的椎体（如下图所示），则所得两个椎体的表面积之和与原圆椎体表面积的比值是（  ）

A．         B．         C．         D．

5．甲、乙、丙三辆汽车分别从A地开往千里之外的B地。若乙比甲晚出发30分钟，则乙出发后2小时追上甲；若丙比乙晚出发20分钟，则丙出发后5小时追上乙。若甲出发10分钟后乙出发，当乙追上甲时，丙才出发，则丙追上甲所需时间是（  ）

A．110分钟         B．150分钟         C．127分钟         D．128分钟

【参考答案】

1．【解析】A。解法一：设重度污染的城市数为x个，则空气质量良好的城市数为（3x+3）个，轻度污染的城市数为2x个。根据题意可列方程x+3x+3+2x=63，解得x=10。所以空气质量良好的城市有10×3+3=33（个）。

解法二：由题意可知空气质量良好城市数是3的整数倍，排除B、C两项。假设空气质量良好城市数是重度污染城市数的3倍，可得空气质量良好城市数︰轻度污染城市数︰重度污染城市数=3︰2︰1，共6份对应63，空气质量良好城市数3份对应31.5，而实际空气质量良好城市数要比31.5大一些，A项符合。

2．【解析】B。设该商品原来的价格为1，则4个商场经过两次价格调整后的售价如下：

甲商场：（1+a）×（l+b）=l+a+b+ab。

乙商场：。

丙商场：。

丁商场：（l+b）×（l+a）=l+a+b+ab。

易知甲、丁两商场两次提价后售价相同，不可能是最高的，故排除A、D两项。比较乙、丙两商场两次提价后的售价，明显有>，即乙商场该商品两次提价后的售价最高。

3．【解析】C。由题意可以得出，193-6=187=11×17，根据11、17均为质数这一特性，要使得黑盒子中的棋子数最少，令白盒子中的棋子数最大=17，则放入后黑盒子中的棋子数=193-17=176，放入前黑盒子中的棋子数=176-15=161。

4．【解析】C。由圆锥体的底面半径为r，母线长为2r，可得圆锥体的表面积为。

所截得的两个锥体的表面积之和要比原圆锥体的表面积多两个等边三角形截面的面积，等边三角形的边长为2r，则其面积为，所以两个锥体的表面积之和为。则两个锥体的表面积之和与原锥体表面积比值是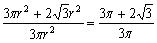。C项当选。

5．【解析】B。设甲、乙、丙的速度分别为、、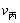，根据追及问题公式有：（-）×120=30、（-）×300=20，整理得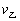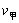（-）︰=1︰4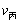，（-）︰=1︰15，令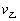=15，则=12，=16。设甲出发10分钟后，乙出发直至追上甲用了x分钟，根据追及问题公式可得（15-12）×x=12×10，解得x=40。可知丙出发时甲已经出发了10+40=50（分钟），那么丙追上甲需要（分钟）。